Produced by OmniGraffle 7.18.5\n2021-12-19 10:04:48 +0000 屏保 Layer 1

小时候的游戏

小时候，我热衷于一类数字游戏，在一堆数字里寻找规律。 比如：1，1，2，3，5，8，13, __?. 答案是 21。所有数字都满足规律：「第三个数字等于前两个数字之和」。

而这个乐于寻找规律的习惯，似乎一直在伴随着我的成长。即使现在，我作为一名初学钢琴的中年人，我仍然对于流淌于音符间的规律感到好奇。于是我便开始用 AI 探索音符间的秘密，并由此诞生了几段 100% AI 创作的旋律：

ckpt28500-pop17-01.mid

ckpt28500-pop17-long-01.mid

其实「AI 作曲」就是一个找规律游戏，在一系列音符的关系中寻找规律，预测出接下来最合适的那个音符。

最终 AI 生成的旋律是由数据、数据 Tokenzie、模型架构、训练以及采样来综合决定。

  • 数据决定了风格：只听过古希腊诺姆音乐的人，是几乎没法写出酒神赞歌的
  • 数据 Tokenzie：如果音符是乐高积木，那么数据 Tokenzie 就是设计这些乐高积木最基础木块。
  • 优秀的模型架构决定了 AI 的学习能力：天资卓越音乐人能举重若轻写出动人心魄的音乐，而平凡如我的普通人则需要百倍的眼界（数据）与努力（算力）。
  • 训练：模型学习成长的过程
  • Sampling（采样）：AI 的预测结果是一堆概率（数字），可以直截了当选取最大概率的音符，亦可以将整体概率分布作为选择依据。

MIDI 与 音乐数据

音乐是一种声音在时间中流动的艺术，并在过程中形成了一种结构。

从物理学出发，声音的实质是传声媒介质点所产生的一系列振动现象的传递过程。而动听的音乐正是一系列质点振动的总效果。 人类可以轻而易举的通过耳膜与「音乐细胞」来感受质点振动的效果，但 AI 没有人类的耳朵，AI 的世界是虚拟化的，组成那个世界的最小「粒子」是数字。

因此，需要一座桥梁，架设在振动与数字之上，连接于现实与虚拟之间。而这座桥梁，早在 1983 就已落成，它就是 MIDI。

MIDI 的全称是「Musical Instrument Digital Interface」，即「乐器数字化接口」。

MIDI对音乐的管理无微不至，即能精细独立的管理乐音的四要素：音高、音长、音强和音色。又有极高的存储效率，200 小时的音乐只要 80M 左右的存储空间。MIDI 所存储的实际只是一组指令，告诉键盘、贝斯、架子鼓等在某个时间以怎样的方式发声。简单来说，MIDI 存储了时间点与音符的对应关系。这与以上 AI 猜音符的游戏不谋而合。

既然 MIDI 很合适，那么把互联网上海量音乐转换成 MIDI 文件，就可以得到充足的数据源。确实如此，但是将网络中 MP3、WAV 等音频转换成 MIDI 的过程也是一个重大挑战。从音频到 MIDI 还需要转录、同步、旋律，和弦提取等。

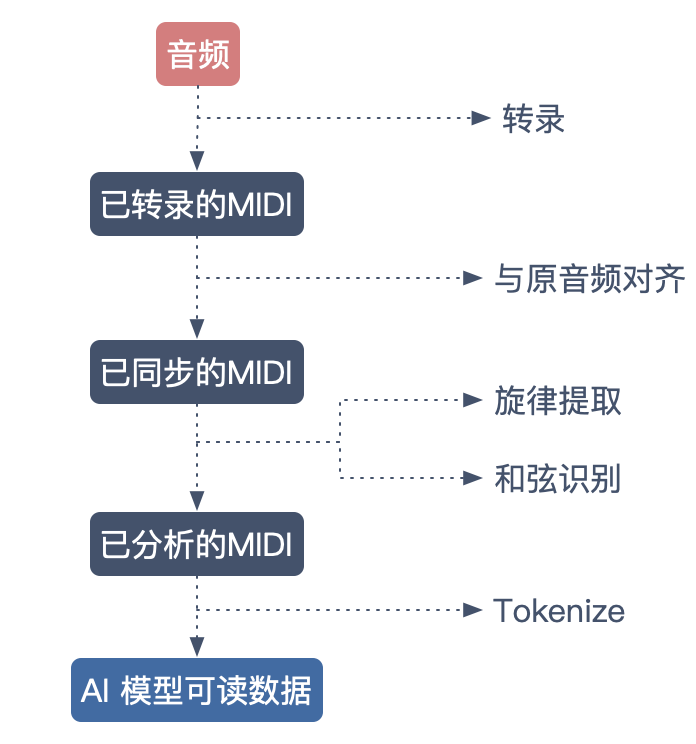
近几年，转录技术迅速发展，为数字音乐提供了大量且优质的 MIDI 素材，2018 的转录还只能从干净的音频信号中提取相对单一的声音。而就在上个月，Google Magenta 团队的最新论文[MT3: MULTI-TASK MULTITRACK][1]，已经对多层次的复杂合奏音频进行转录。（ 转录技术不是本文重点，感兴趣的朋友推荐阅读文末 [1]。 ） 本文所用的数据源来自 aiLabs.tw 团队的 Pop1K7 数据源。

MIDI Tokenzie

如果音符是乐高积木，那么 MIDI Tokenzie 就是设计这些乐高积木最基础木块。

在乐理知识中，一首曲子的元素离不开：小节、节奏、音高、音长等等。MIDI Tokenzie 正是定义了这些元素的最基本「小木块」，每首曲子都是「小木块」的有序组合。

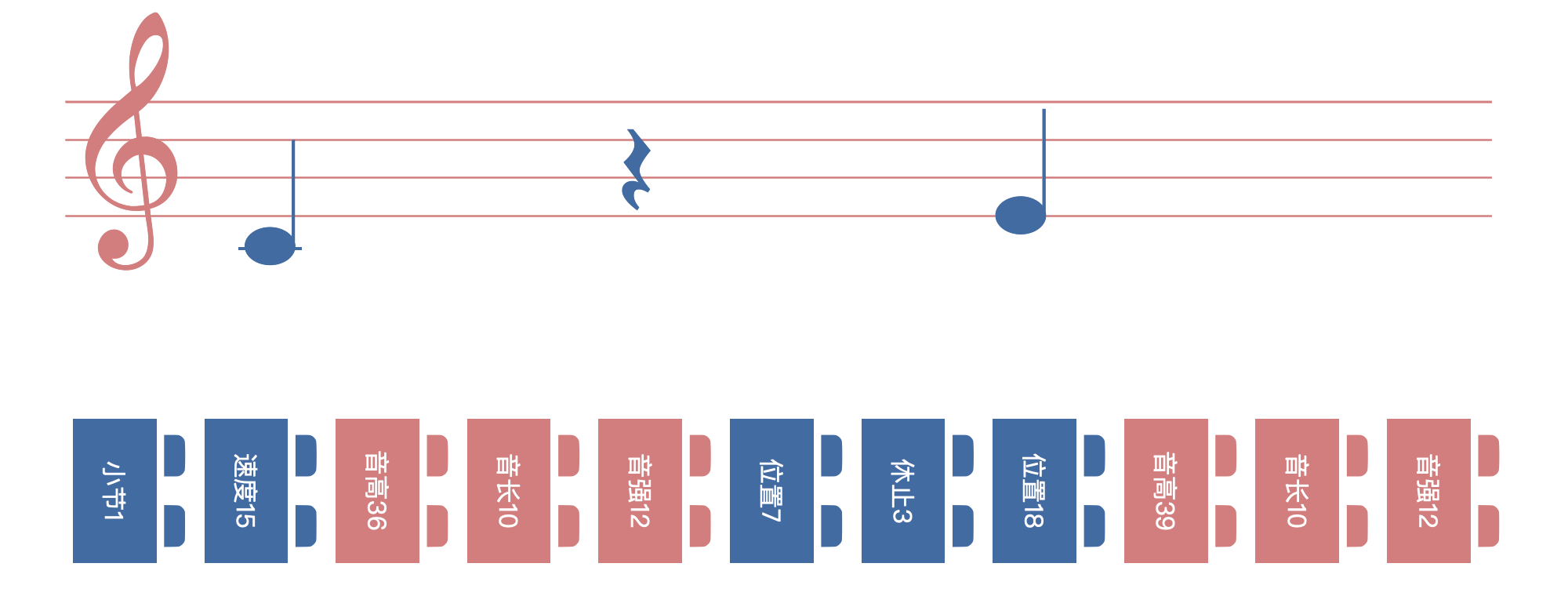
一种叫 REMI[2] 的 MIDI Tokenzie 方式。就是把 MIDI 按照如下几个纬度打散拆分：

  • 小节/位置（Bar/Position）: 把一个小节的长度平均分成 32 份，每一份代表该小节中的一个位置。 每个「小木块」分别用 [1~32] 表示。
  • 速度（Tempo）：从慢到快，平均拆分成 32 种速度。数字范围[33~64]。
  • 音高 (Pitch)：钢琴的 88 个键各自为独立音高。「小木块」范围[65~152]。
  • 音长（Duration）: 从短到长，平均拆分成 64 种音长。「小木块」范围[153~216]。
  • 音强（Velocity）: 从轻到重，平均拆分成 64 种音强。「小木块」范围[217~280]。
  • 休止（Rest)）: 从轻到重，平均拆分成 10 种音强。「小木块」范围[281~291]。 如此一来，一段旋律就可以用一段数字序列来表示了。

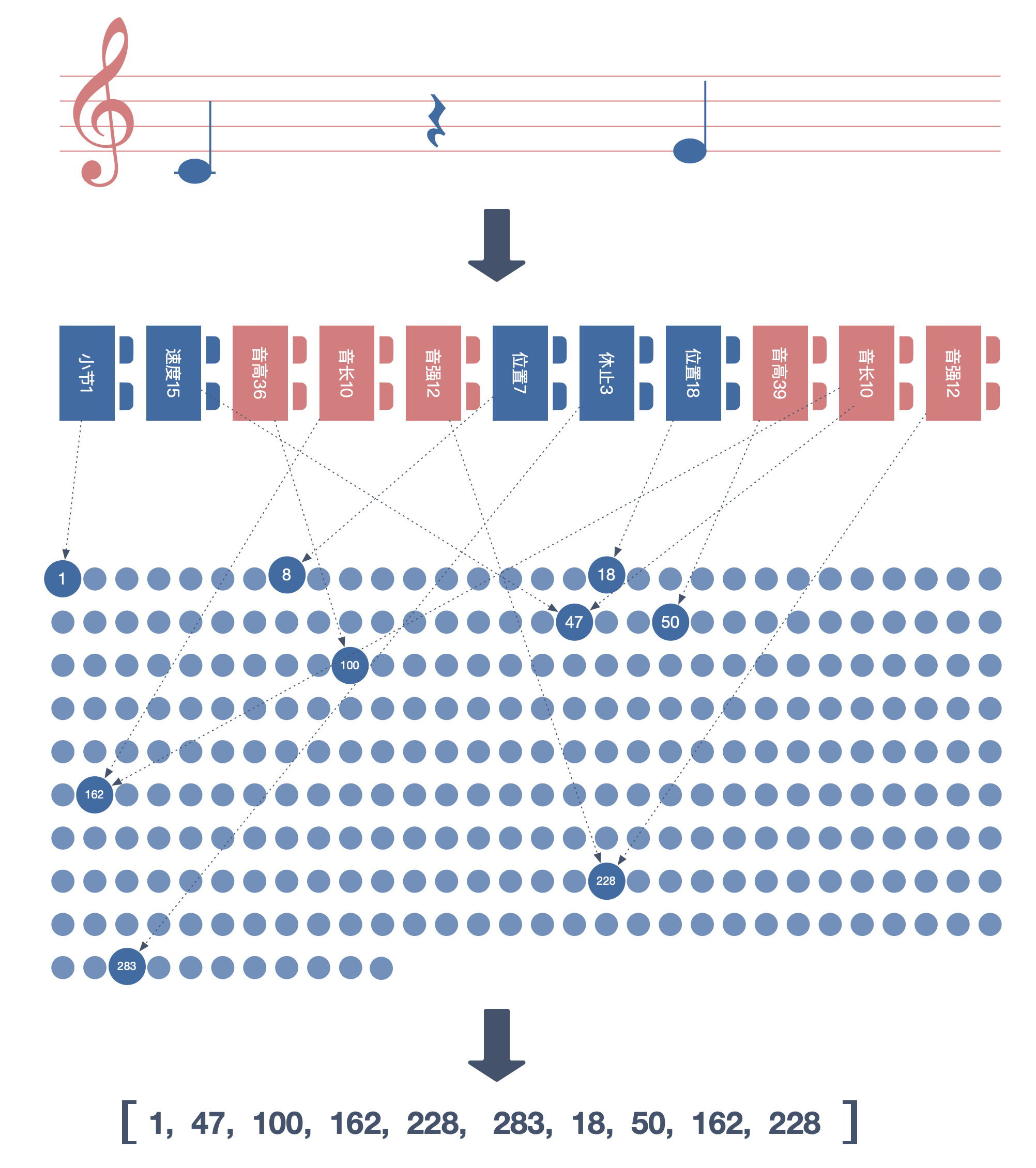
MIDI Tokenzie 是把现实里「杂乱无章」的振动映射成连绵不绝的数字，那是 AI 才能听懂的「音乐」。

「AI 作曲」的模型

AI 模型是一个装有神经元的盒子。与人类的神经元不同，AI 的神经元是计算机的模拟。人类的神经元通过突触间的电流传达一种刺激，而 AI 神经元通过一个简单的公式 $w*x+b$ 传递数字。

旋律被 MIDI Tokenize 得到数字。丢进盒子之后被神经元接收，经过亿万神经元的有序传递，最终输出新的数字。这些新的数字可以重新转换成 MIDI 文件，变成 AI 创作的音乐。

计算二者关系要考虑所有维度。而 AI 就如同一名冷峻的猎手，依靠他百眼巨人强大观察力，能够在千百维度之中，捕获音符数字间流淌的微妙关系。

这这种能力离不开一个重要的机制，即来自于 Google 的那篇著名论文 Attention Is All You Need[3]。 论文的核心就是 Attention 机制，源于对生物行为的模仿，即用算法模仿了生物观测行为的内部过程，依据外在刺激与内在经验，增强局部的观测精度。就好比人类在集中观测某个具象物体时，无关的画面会自动模糊。

如今 Attention 机制已经深入到各个领域的 AI 算法中，就连即时战略游戏中那些战无不胜的 AI，支撑它们的算法都离不开注意力机制。比如《星际争霸2》的 AlphaStar，《Dota2》的 OpenAI Five 等等。

[AI 作曲]模型的核心之一，就是 Attention 机制**

假设AI 在 256 个维度下捕获数字间的关系。那么每个数字就要在 256 个维度下展开。 比如 「音高36」所对应的数字 100 ，数字 100 会被展开 256 个精度极高的浮点数。每个浮点数都代表了数字 100 在该维度下的值。

同样的，如果把一组「小节 速度 音高 音长 音强」 丢进盒子，就会得到 5 组 256 个浮点数。

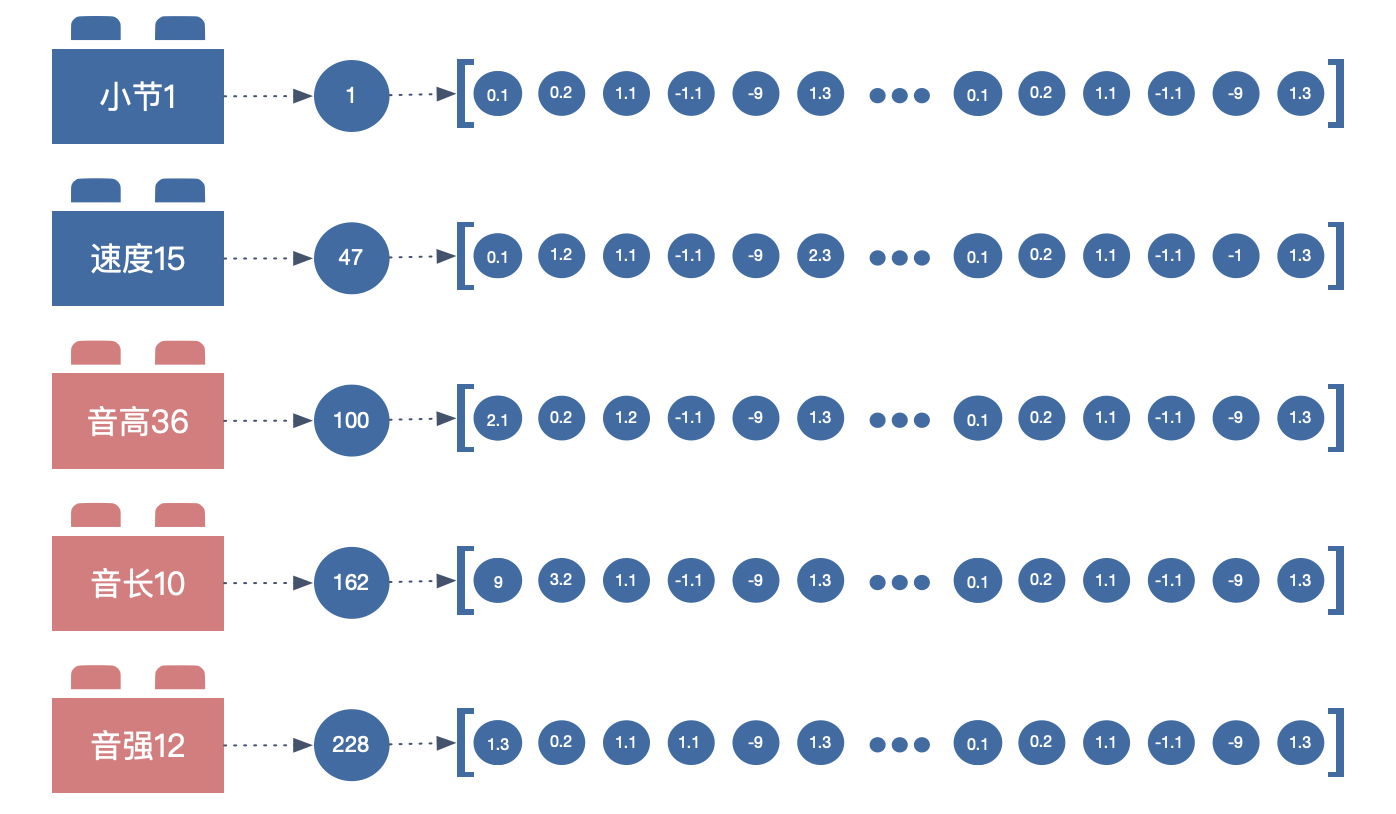
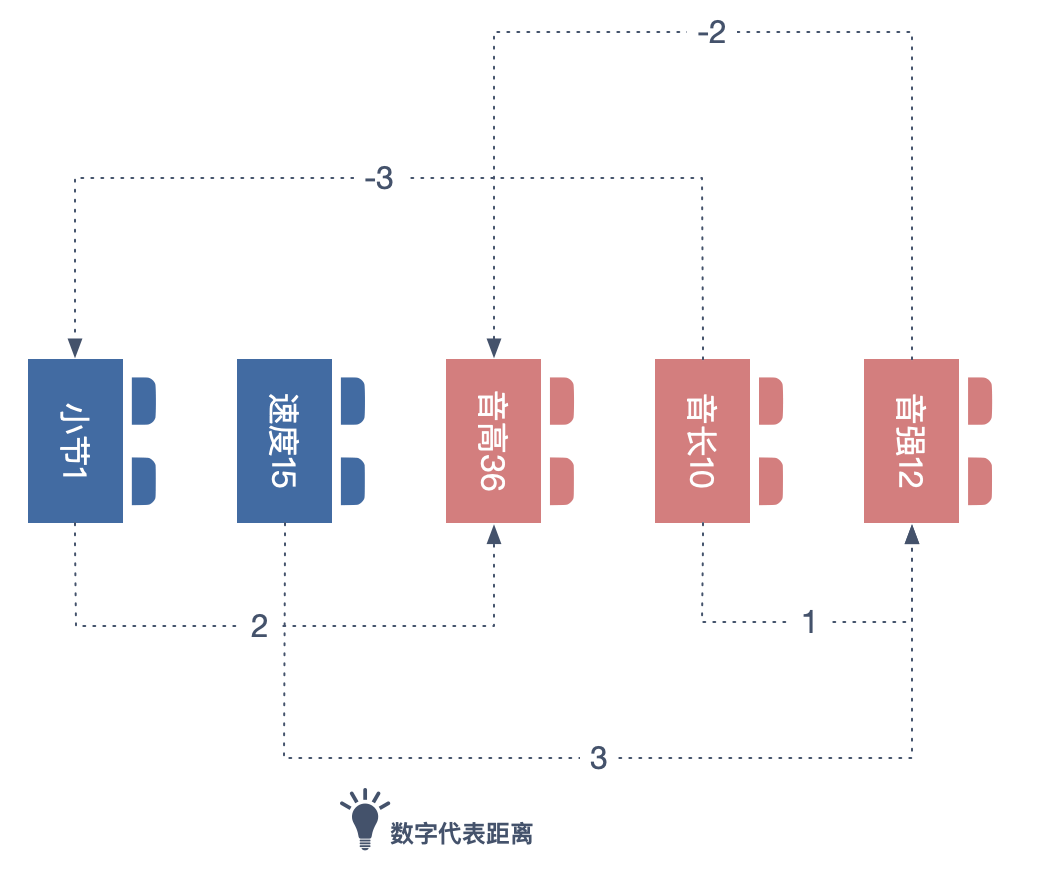
Attention 机制的关键一步，就是把分别把每组数字与其它组数字依次做线性代数点积的运算，这就相当于把 256 个维度的每一个都纳入了考量。 比如分析「小节1」与「音高36」间关系，可将二者的所展开的浮点数做点积运算。

$小节•音高 = 0.1×2.1+…+1.3×1.3$

得到的点积结果，在一定程度上包含二者的关系。以上是对 AI 捕获个体关系的一个基础理解，Attention 正是一系列这种关系捕获方式的组合。感情兴趣的朋友可参看相关资料。

[AI 作曲]模型的核心之二，Relative Attention（相对位置的注意力机制）

它是在 Attention 机制之上做进一步调整。Attention 机制虽然可以寻找各个音符之间的关系，但对于音乐，还要考虑的就是旋律的周期性与规律性。因此，音符之间的相对位置也要纳入权重影响的考量。这也是论文 [Music-Transformer][4] 中所提及的关键一步。将各个音符之间的相对位置也纳入考量的 Attention 就是 Relative Attention。

比如以一段旋律作为开头，延续作曲。采用 Attention（无 Relative），生成的旋律一分钟后会很容易「糊掉」。 而采用 Relative Attention ，可以输出几乎长度无限，且颇具变化性的旋律。

一段36分钟的旋律 – AI-Music-Long-03

Relative Attention 具体实现，请参考文末源代码链接。

[AI 作曲]模型的核心之三，Compound Word Transformer**

Compound Word Transformer[5] 这篇论文发表于在 2021.1，该论文提出的模型，训练效率大幅提升，能达到了 2018 年 [Music Transformer]的 5~10 倍，且生成的旋律也有了更好的表现。（文中开头的音乐就是用基于 Compound Word Transformer 的模型生成。）

Compound Word Transformer 的优异表现，来自于一项重要改进。即将类 REMI MIDI Tokenize 的串行输入方式，变成了 Compound Word MIDI Tokenize 的并行输入方式。

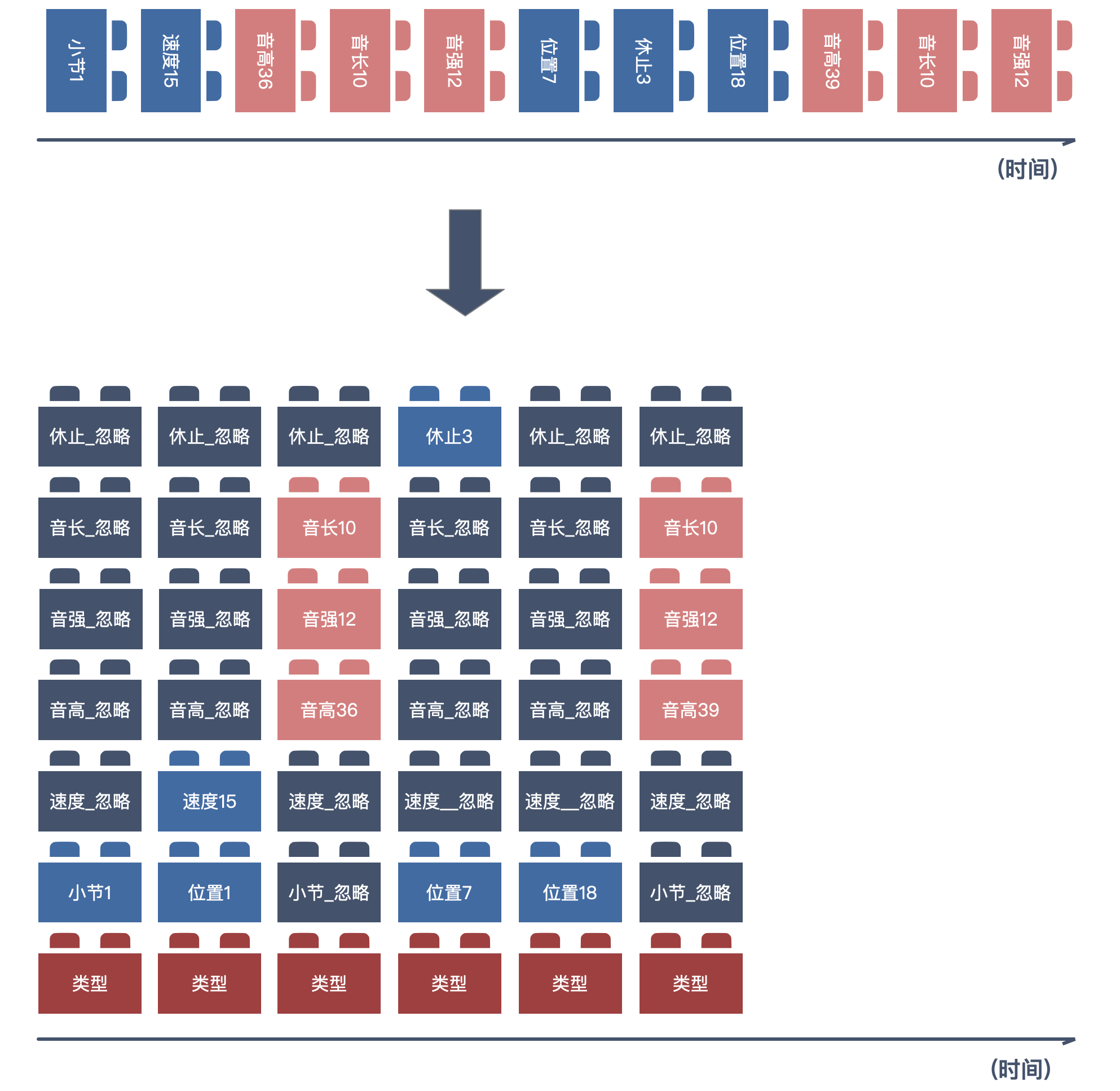
这种并行的输入方式，会带来几个显著的好处：

  • MIDI Tokenize 之后的序列长度大大压缩，这将更有利于训练的拟合，且有利于生成更长时间的旋律。
  • 模型支持给予音高、音长、音强、休止符等不同的权重的训练参数。比如，音高的展开 1024 维，休止符的展开 256 维。
  • 训练过程中，不同的音乐元素可以被独立的监测训练效果。
  • 得到结果后，最终可以分别对音高、音长、音强、休止符等等采取不同的采样策略。比如让音高、音长变化较多，音强变化较少。

那么 Compound Word Transformer 为什么能可以支持并行输入，做个简短解释：Compound Word Transformer 用了一系列的线性变换的技巧，将 Tokenzie 结果的并行结构变换成串行结构，之后再丢给 Attention 捕获关系，得到串行结构的结果之后，再用线性变换的技巧，将结果转成并行结构作为输出。

Compound Word Transformer 是我最终使用的模型，因为论文较新且资源不多，一路上走的踉踉跄跄，摸索实现的代码（Tensorflow 版）已开源在 Github，点击查看原文。

训练

阿尔戈英雄必须不断的战胜玻俄提亚土地中生出的龙牙武士，才能最终夺取克律索马罗斯的金羊毛。

AI 模型的训练过程，就如同一个要不断战胜龙牙武士的 RPG 游戏，每点经验值，都是对亿万神经元间连接权重的一次优化。 训练「AI 作曲」的模型，用动听的旋律作为输出标准，AI 反向调整自身参数，这就是深度学习领域的反向传播。 AI 输出的音乐与训练数据的音乐之间总是会有「差距」，我们把这个差距的叫做 LOSS。训练的目标之一就是让 LOSS 变小，就如同消灭龙牙武士一样。

LOSS 是由亿万变量所决定的，那么 AI 如何得知 LOSS 变小的方向。其实也很简单，建立 LOSS 与 亿万变量的函数关系。

$$LOSS=f(x_1,x_2,…,x_{10000})$$

让 LOSS 对每个变量求一次偏导数，这样就知道了每个参数对于 LOSS 的影响方向，再让所有参数都沿着 LOSS 变小的方向移动一点点，得到的新的参数。这个过程在深度学习中叫一个 STEP，是模型反向传播自我学习的过程。

训练开始后，随着 STEP 的增加，模型对于训练集的精度逐步走高，验证集的精度则是先高后低。这是由于模型慢慢的进入到一种过拟合的状态。

因此要选择出一个模型效果最佳的 STEP 点。通过实验发现，生成音乐效果最好模型，往往都发生在验证集最佳点之后。比如本人得出的最佳模型在 STEP == 28500，这之前的模型（STEP10000）生成的旋律会显得过于轻飘，或者说「不在调上」，而这之后的模型（STEP10000）所生成的旋律会显得「缺少变化」。

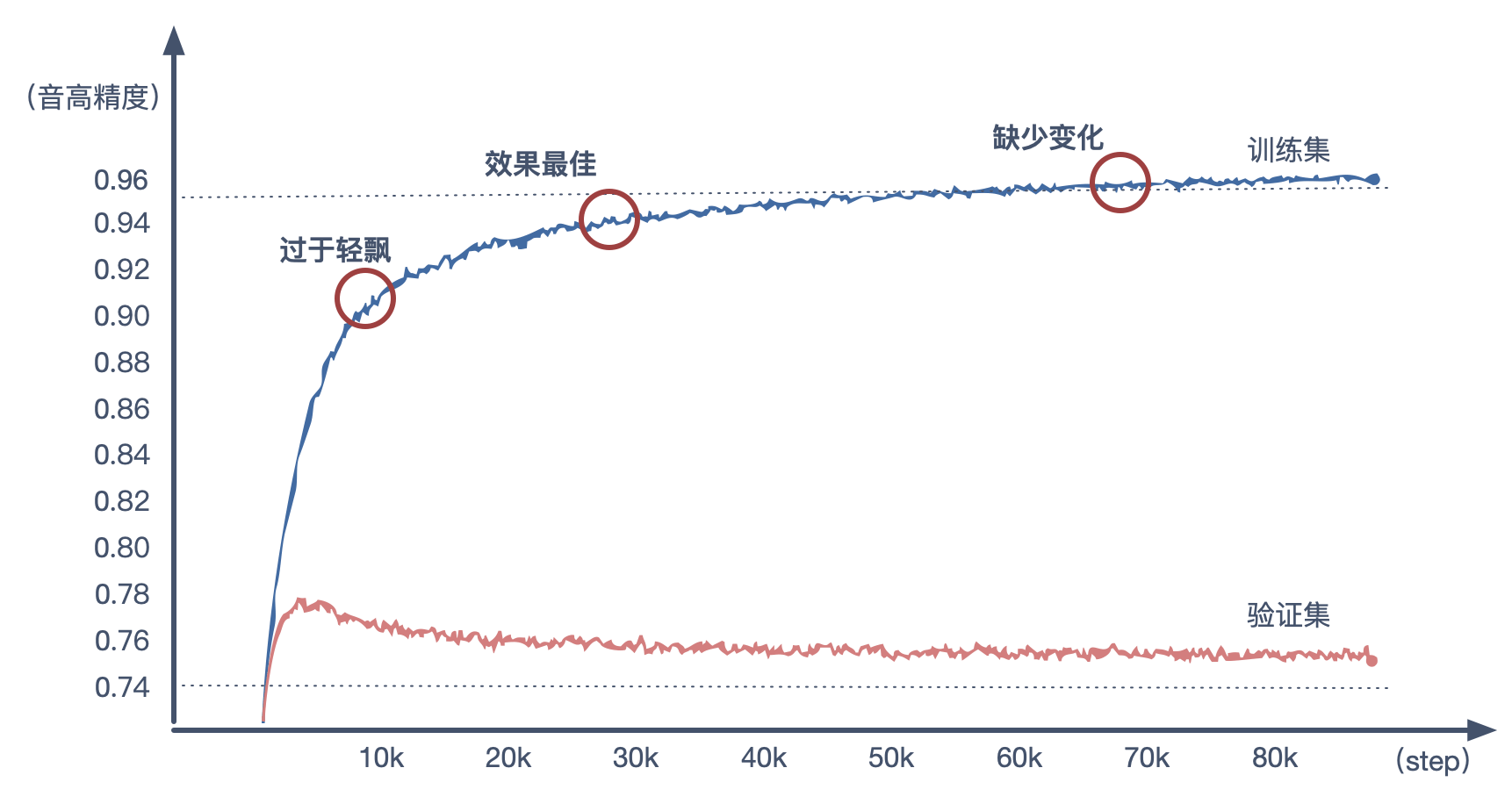
比如对给定开头的三段旋律

STEP10000 生成（过于轻飘）

STEP28500 生成（恰当好处）

STEP80000 生成（缺少变化）

当然，最终理性数字所标记的精度，只能表达模型对于训练集的拟合程度，不能标记音乐感性的动听程度，音乐感受是因人而异的主观体验。 以上为个人训练经验，仅供参考。训练细节在源代码中有详细说明（点击原文查看）。

Sampling（采样）

AI 最终给出的数字，即是概率分布。而Sampling 就是从特定的概率分布中选取样本的过程。对于 「AI 作曲」，Sampling 算法就是从音符的概率分布中挑选音符的规则。一个很自然的思路，直接使用 Greedy Search（只选择概率最大的）。

在实际的测试中发现， Greedy Search 会导致音乐缺少变化，甚至陷入一种永不回转的单调。这是一种 「Get Stuck In Loops」现象。

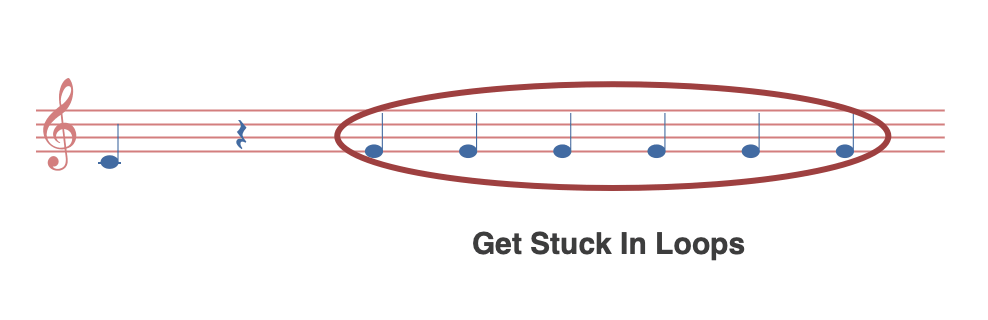
对于解决 「Get Stuck In Loops」现象 ，Temperature Sampling（温度采样）是个不错的选择。该算法是将概率分布做一次 softmax（即将是所有的概率压缩在$(0,1)$ 之间，且相加之和等于1） ，得到概率分布$P$ 。 再用 $P$ 除以温度 T（自定义参数）得到$P_新=P/T$，最后对 $P_新$ 做一次概率取值。

一个简单的理解，是把结果的概率分布想象成一座连绵起伏的冰山，温度升高，冰山就会融化，那么概率之间就会更加接近，极限高温时，所有的概率间将无差别。因此说，温度越高概率的分布越平缓，温度越低概率分别将更为集中，温度 1 时，概率分布保持原样。 有了温度调节之后，旋律可变性就有一定的调整空间了。但仍不高效，因为一系列概率极小的长尾作为一个群体也有可能被选中，这会影响最终效果。

进一步升级，将 TOP-P Sampling 与 Temperature Sampling 结合的算法，这也是我最终采用的是采样方式。

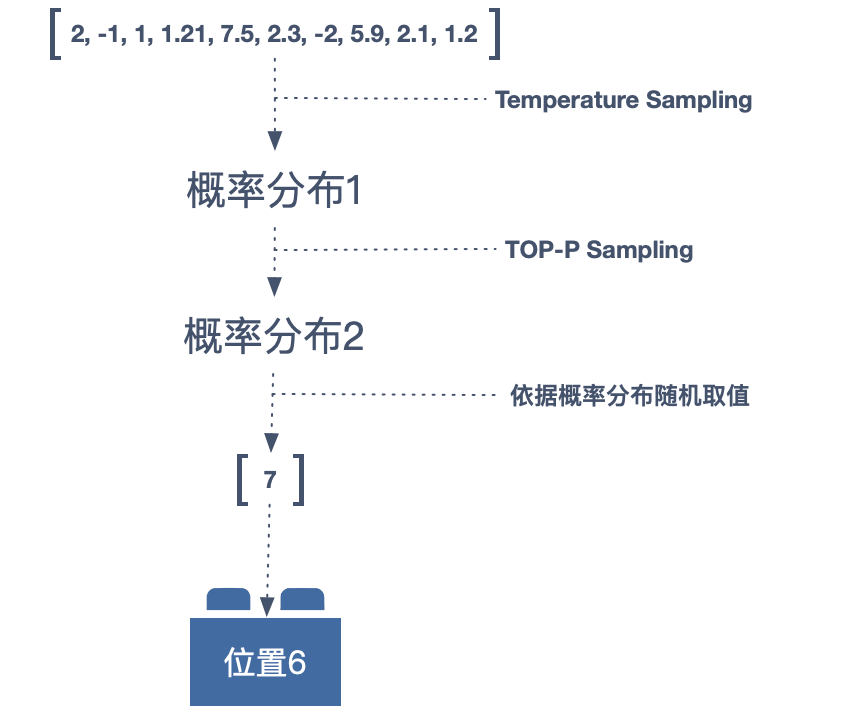
TOP-P 算法的核心思路就是丢弃掉那些末尾的小概率结果。就比如美国大选并不是所有美国公民都是候选人。TOP-P 便可通过设置 P 的数值，来决定末尾概率的忽略程度。P 的值越大，忽略的程度越低，当 P 为 1 时，会保留所有概率，这时就与 Temperature Sampling 无差别了。而在实际的操作中，我会对不同的音乐元素设置不同的 T（温度）与 P，比如，将 Duration（音长） 的 T 和 P 都设高些，以便让旋律获得更多的变化，而将 Bar(小节)的 T 与 P 设低一些，让旋律保持一定稳定性。

以下两首是为相同开头续作，对比 「T-音高」不同的旋律。

T-音高 == 1

T-音高 == 0.1

第一首（T-音高=0.01）的音高会保持较好的前后一致性。而第二首（T-音高=1）的旋律则相对有了更加灵动多变的感觉。

Produced by OmniGraffle 7.18.5\n2021-12-19 10:04:48 +0000 屏保 Layer 1

美不能被量化，但却有迹可循。AI 三脚猫功夫般的作曲，即是一种证明。

古人所云的“唯乐不可以为伪”，是把音乐作为一种极致感性的表达。即使谎话连篇的音乐人，其作品也必定融入真情实感。「多的是，你不知道的事」，确实，在音乐的世界里，他讲了真话。

而 AI 作曲，是理性世界向感性世界发起的挑战，是一种用一元论统一世界的企图。如果动物的真情实感都可以被 AI 所模拟，那么终有一天，我们就能创造出一个优化在现实之上的虚拟世界，这或是一种形式的永生。我们将摆脱肉身的累赘，把那些山呼海啸的所思所想，那些分分秒秒积累的平凡记忆，都工工整整的写进一张可插入机械身躯的卡片里。就像把备份好的 sim 卡插到新手机里一样容易。 但是，世界未必是一元的，情感与意识也未必由物质所决定，当下没有人知道正确答案，这是物理学的极具，基础物理已经百年未有大的突破了。

当经济发展的红利榨干了内卷空伐的身躯之时，浮皮潦草的娱乐就会伺机占领人的闲暇生活。时代的发展值得怎样程度的个人付出，这是需要去思考的问题。但毋庸置疑的是，这个时代仍然需要一只砸中下一个牛顿的苹果，需要一颗仅凭借思考就将广义相对论应用于建立宇宙模型的大脑，更需要一朝比雅典娜相助的尔戈英雄们还要更多的气运。

AI 与艺术的融合虽更依赖基础科学的突破，但美的确有迹可循，即当下 AI 创造的艺术作品也是丰富多彩的。这是科技与艺术融合的极佳领域，也是统一数字与情感的探索路程。

窗外的梧桐树渐渐露出条理清晰的枝条，窗前的小野猫发现了投放罐头的规律，这八个月的学习时光使我充实，并由此生出一种即熟悉又遥远的奇妙感受，我想了很久，直到开始写这篇文章时我才摸索到知晓中的记忆，原来这奇妙的感受源自我无所忧虑的年少时光，源自那个一筹莫展的小男孩在浩如繁星的数字间抓到规律时，由心底升起的那份似如月光般清朗真切的快乐。

sound_and_music_computing(AI+音乐) Telegram Group

近来有些私信我的小伙伴，希望建立一个 「AI 音乐」微信群。我考虑了一下，决定建立一个 tg 群，主要讨论算法音乐以及相关的音频技术。欢迎对 AI 音乐有兴趣的小伙伴加入讨论，一起学习。

https://t.me/sound_and_music_computing